4.2        OLCR measurement of the complex impulse response

4.2.5       OLCR measurement of FBG

We have now all the information required to derive the OLCR response of a FBG. The positions and physical distances are those indicated in Fig. 4-5. The spectral response to a stationary lightwave of a FBG at its entrance is given by the complex spectral function r_fbg(n) that can be calculated by T-Matrix method (chapter 3, §3.1.4). The electric field E_r from the reference arm on the detector is given by

where E_s is the source field, 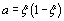, x and (1-x) are the intensity transmission coefficients of the coupler and R is the intensity reflection coefficient of the reference mirror. The test electric field E_t is given by

where the propagation constant is only developed to the first order (that is : D_n = 0) and using equations (4-20) and (4-21a), the following equation is obtained :

As seen in §4.2.4, Dn = (n(n)-n_g(n)). The intensity I(z) measured by the detector is then

The constant intensity factor I_dc is

The modified coherence function 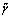and the AC amplitude I_ac are found to be

where h_fbg(t) is the FBG impulse response in reflection (Fourier transform of the complex reflection amplitude r_fbg(n)).

The OLCR signal is defined as the interfering part of I(z), that is 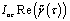. Considering a 3 dB coupler (a = 0.5), a perfect reflecting reference mirror (R = 1) and neglecting the phase factor exp(i2d_tk₀Dn), the equation (4-2) is obtained. The OLCR signal is related through the grating impulse response amplitude h_fbg(t) to the reflection amplitude r_fbg(n) and for this reason the logarithmic scale representation is defined as

where the factor 20 takes account for the amplitude signal.

The resolution in the fiber is defined as half the coherence length in the fiber

For a Gaussian light source centered at 1300nm with a spectral width of 40 nm propagating in a single mode fiber with n = 1.45, we find a resolution of L_r = 12.8 mm.